正五角形の作図
うちの子に数学を教えている。
算数を教えたのがつい昨日のようだ。
折角、復習したので、どこかに書き留めておきたい。
はっきりいって他のテキストの方が詳しくて丁寧で分かり易いと思う。
まずは駆け足で正五角形の作図まで行って、その後内容を充実したい。
高校数学は、x5=1 の解に始まり、z5=1 の解に終わる。
すなわち、因数分解に始まり、オイラーの等式(博士の愛した数式)に終わる。
因数分解
上式を移項すると x5−1=0 であるが、
xn−1 を因数分解すると次の通り。
x2−1=(x−1)(x+1)
x3−1=(x−1)(x2+x+1)
x4−1=(x−1)(x3+x2+x+1)
x5−1=(x−1)(x4+x3+x2+x+1)
よって、解のひとつは x=1 である。
xn=1 の解なのだから当たり前である。
「他に解は無いのか?」という疑問が五角形の作図へ繋がる。
二次方程式の解
今の中学ではいきなり暗記させるだけで導かないらしい。
なので、ざっくり導いておく。
二次方程式の一般解は次の通り。
ax2+bx+c=0
x2+bax+ca=0
x2+bax=−ca
x2+bax+b24a2=b24a2−ca
x2+2(b2a)x+(b2a)2=b24a2−4ac4a2
(x+b2a)2=b2−4ac4a2
x+b2a=±√b2−4ac4a2
x=−b2a±√b2−4ac2a
x=−b±√b2−4ac2a
よって、解を x1,x2 とすると、因数分解は次の通り。
ax2+bx+c=a(x−x1)(x−x2)
二次関数
二次関数 y=ax2+bx+c は放物線を描く。
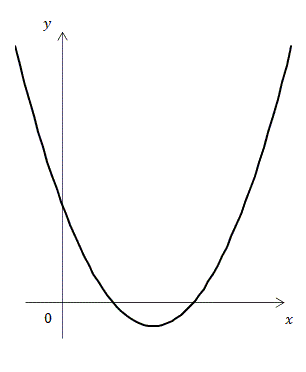 y=0 となる箇所、すなわち x 軸との交点が上述の x1,x2 となる。
y=0 となる箇所、すなわち x 軸との交点が上述の x1,x2 となる。
判別式 b2−4ac が負のときは
交点を持たず
y=0 となる様な x の解は無い。
「本当に解は無いのか?」という疑問が五角形の作図へ繋がる。
その他の関数・絶対値・ガウス記号など
|x|、[x]、など。省略
不等式
≠、<、>、≦、≧、相加平均・相乗平均など。省略
集合
逆・裏・対偶など。省略
会社にも居るよね。言われたことの逆や裏を駄目だと思い込んじゃう人。
大抵は間違ってるが、命じた側も逆・裏が分かってないから訂正できない。
JKの「逆にぃ~」も気になる。会話を聞いてると逆じゃないじゃんと思う。
素数
素因数分解・最小公倍数・最大公約数など。省略
合同式
剰余について。省略
順列・組合せ
n 個の中から r 個選ぶ順列 nPr は、
n 個の中からひとつ選び、残った n−1 個の中からひとつ選び、残った n−2 個の中から…を r 回行なう。
nP r=n!(n−r)!
n 個の中から r 個選ぶ組合せ nCr は、
r 回の内での順番を考えない。
nC r=nPrrPr=n!r!(n−r)!
二項定理
(x+y)n を展開(二項展開という)すると次の通り。
(x+y)0=1
(x+y)1=x+y
(x+y)2=x2+2xy+y2
(x+y)n=a0xn+a1xn−1y+a2xn−2y2+…+an−2x2yn−2+an−1xyn−1+anyn
係数 ak(二項係数という)はパスカルの三角形になる。
ak={ 1 (n=0) 1 1 (n=1) 1 2 1 (n=2) 1 3 3 1 (n=3) 1 4 6 4 1 (n=4)1 5 10 10 5 1 (n=5)
n 次の行の値はひとつ上の行の2値の和
あるいは (x+y)n=(x+y)(x+y)(x+y)…(x+y) であるから、
最初の括弧から x or y を選び、
次の括弧から x or y を選び、
の組合せなので次の通り。
(x+y)n=nC 0 xn+nC 1 xn−1y+nC 2 xn−2y2+…+nC n−2 x2yn−2+nC n−1 x yn−1+nC n yn
統計
平均・偏差・分散・標準偏差・相関係数など。省略
確率分布
一様分布・二項分布・正規分布など。省略
指数法則
xn を x の n 回の積と定義する。
x1=x
x2=x×x
x3=x×x×x
すると、次の法則が成り立つ。
xm×xn=xm+n
xmxn=xm−n
上の法則が成り立つ様に定義域を拡張する(ただし x≠0 のとき)
x0=1
x−n=1xn
また、次の法則が成り立つ。
(xm)n=xm×n
上の法則が成り立つ様に定義域を拡張する。
x1/n=n√x
最初の定義域は自然数であった。
次に定義域を整数に拡張した。
その次に定義域を実数に拡張した。
有理数だけじゃないか?無理数はどうした?というツッコミは無視する。
有理数で定義されたモノは無理数でも自動的に適用されるのだ。
定義域を外れるので、最初の定義からは x0=1 の証明はできない。
x0=1 としても最初の定義とは矛盾しないことが示せるだけである。
最初の定義と矛盾しない様に、定義域を拡張したのである。
例えば 00 は、
文脈によって 0 と定義されたり 1 と定義されたり、
不定義とされたりする。
ここでいいたいのは、簡単なルールを決めてそれを使っているうちに、
もっと広い世界に気付き、ルールが拡張されるということである。
「00 は何なのか?」という疑問が五角形の作図へ繋がる。
平行線の公理
省略
ここでは略すが、三角形を説明するなら、ここまで遡るべきだろう。
中心角・円周角
省略
ここでは略すが、正弦定理・余弦定理を説明するなら、ここまで遡るべきだろう。
ピタゴラスの定理(三平方の定理)
省略
なんとなくノリで挙げてみた。
ベクトルを説明するなら、ここまで遡るべきだろう。
三角関数
直角三角形で、角度 θ における辺の比を次の様に定義する。
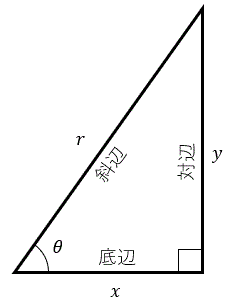 斜辺に対する対辺の割合(正弦ともいう)
sinθ=yr
斜辺に対する底辺の割合(余弦ともいう)
cosθ=xr
底辺に対する対辺の割合。すなわち傾き
tanθ=yx
対辺に対する底辺の割合。つまり上記の逆数
cotθ=xy
しかし、この定義だと角度が0~90°の範囲しか扱えない。
斜辺に対する対辺の割合(正弦ともいう)
sinθ=yr
斜辺に対する底辺の割合(余弦ともいう)
cosθ=xr
底辺に対する対辺の割合。すなわち傾き
tanθ=yx
対辺に対する底辺の割合。つまり上記の逆数
cotθ=xy
しかし、この定義だと角度が0~90°の範囲しか扱えない。
円で、半径に対する長さの比で再定義する。
すなわち、単位円(半径1の円)で拡張定義する。
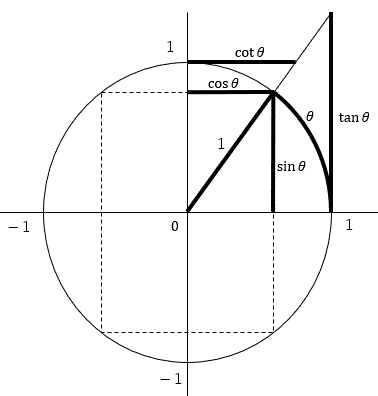 角度を半径に対する弧長の比で示す。
角度は1周に対する割合であり、無次元量である。
1周を360°として表してもいいし、
1周を 2π として表してもいいし、
1周を100%として表してもいい。
角度を半径に対する弧長の比で示す。
角度は1周に対する割合であり、無次元量である。
1周を360°として表してもいいし、
1周を 2π として表してもいいし、
1周を100%として表してもいい。
もっとも「角度」を%表記するのは円グラフのみであって、
通常は「傾き」を%表記することが多い。
碓氷峠の66.6‰(パーミル)は1km進むと66.6m登る傾き。
角度と傾きを混同しないこと。
角度を傾きに換算する関数が tanθ である。
定義より幾つかの関係式が得られる。
sin2θ+cos2θ=1
tanθ=sinθcosθ
{sin(θ+2π)=sinθcos(θ+2π)=cosθtan(θ+2π)=tanθ
{sin(θ+π2)=cosθcos(θ+π2)=−sinθtan(θ+π2)=−1tanθ
高校では扱わないことになっているが大学入試で平気で使うもの
{cscθ=1sinθsecθ=1cosθ
また、y=sinθ、x=cosθ のとき
{θ=arcsinyθ=arccosxθ=arctanyx
正弦定理・余弦定理
省略
本当に略していいのか?私は2次元に限れば行列の方が好きなので略していいのだ。
奇関数・偶関数
f(−x)=−f(x) を奇関数、
f(−x)=f(x) を偶関数という。
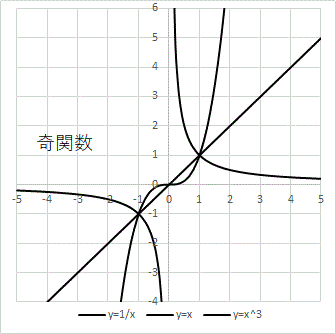
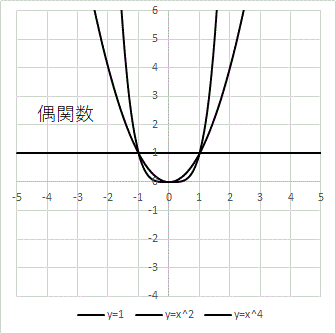 奇関数はグラフが原点対称であり、
偶関数はグラフが y 軸対称である。
奇関数はグラフが原点対称であり、
偶関数はグラフが y 軸対称である。
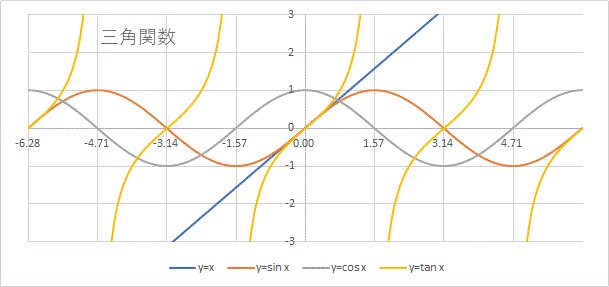 sinx は奇関数、cosxは偶関数、tanx は奇関数である。
sin(−x)=−sinx
cos(−x)=cosx
tan(−x)=−tanx
sinx は奇関数、cosxは偶関数、tanx は奇関数である。
sin(−x)=−sinx
cos(−x)=cosx
tan(−x)=−tanx
行列(マトリックス)
今の高校では行列を扱わないらしいので、ざっくり記しておく。
こんなもんは専門書を読む方が詳しい。まぁ、ただの自己満足である。
縦横に値を並べたものを行列という。ただそれだけ。
例えば次の様に、連立方程式を行列で表すことができる。
{ax+by=cdx+ey=f⟹(abcdef)
例えば座標は1行(または1列)の行列である。
(x,y,z) または (xyz)
スカラー・ベクトル・テンソル
大きさのみの量をスカラーという。
単独の値で記述する。
例えば圧力。
x
大きさと向きを持つ量をベクトルという。
座標の形式で記述する。
例えば力。
(x,y,z)
複数のベクトルで表される量をテンソルという。
行列の形式で記述する。
例えば応力。固体は縦に引っ張りつつ横に圧縮することができ、
断面方向によって異なる圧力(応力という)となるので、
応力はスカラーやベクトルでは表現できない。
(x1y1z1x2y2z2x3y3z3)
さて、もう一度。
スカラーは単独の値で表される量である。
x
ベクトルはスカラーの並びで表される量である。
横一列(または縦一列)の値の並びで記述する。
スカラーは1次元のベクトルである。
(x1,x2,x3)
2階のテンソルはベクトルの並びで表される量である。
縦横の値の並びで記述する。
スカラーは0階のテンソル、ベクトルは1階のテンソルである。
(x11x12x13x21x22x23x31x32x33)
3階のテンソルは2階のテンソルの並びで表される量である。
行列では手に負えないので、要素に添字を3ヶ使って記述する。
(xijk)
以下同様に n 階のテンソルは要素の添字を n ヶ使って表される量である。
ベクトルの加法・減法
スカラーの足し算は次の通り。演算結果もまたスカラーである。
 ベクトルの足し算は次の通り。演算結果もまたベクトルである。
ベクトルの足し算は次の通り。演算結果もまたベクトルである。
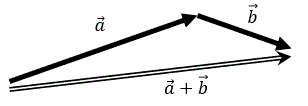
さて、もう一度。
ベクトルの足し算は次の通り。
 (ax, ay)+(bx, by)=(ax+bx, ay+by)
ベクトルの引き算は次の通り。
(ax, ay)+(bx, by)=(ax+bx, ay+by)
ベクトルの引き算は次の通り。
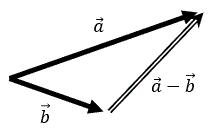 (ax, ay)−(bx, by)=(ax−bx, ay−by)
なお、交換法則が成り立つ。
→a+→b=→b+→a
また、スカラー倍が可能である。
→a+→a=2→a
(ax, ay)−(bx, by)=(ax−bx, ay−by)
なお、交換法則が成り立つ。
→a+→b=→b+→a
また、スカラー倍が可能である。
→a+→a=2→a
ベクトルの内積・外積
→a と →b の 平行成分同士の積を内積 →a⋅→b という。
演算結果はスカラーである。
仕事=距離・力に対応する。
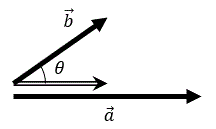 →a と →b の成す角を θ とするとき
→a⋅→b=|a||b|cosθ
なお、cosθ は偶関数なので θ の向きは関係ない。
→a と →b の成す角を θ とするとき
→a⋅→b=|a||b|cosθ
なお、cosθ は偶関数なので θ の向きは関係ない。
よって、交換法則が成り立つ。
→a⋅→b=→b⋅→a
また、分配法則が成り立つ。
→c⋅(→a+→b)=→c⋅→a+→c⋅→b
よって
(ax, ay)⋅(bx, by)=axbx+ayby
→a と →b の 垂直成分同士の積を外積 →a×→b という。
演算結果は2次元ではスカラーとして扱える。
トルク=距離×力に対応する。
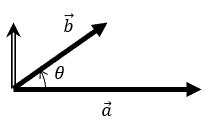 →a と →b の成す角を θ とするとき
→a×→b=|a||b|sinθ
なお、sinθ は奇関数なので(x 軸方向から y 軸方向を正回転として)θ を式の順に →a から →b の向きとする。
→a と →b の張る平行四辺形の符号付き面積となる。
→a と →b の成す角を θ とするとき
→a×→b=|a||b|sinθ
なお、sinθ は奇関数なので(x 軸方向から y 軸方向を正回転として)θ を式の順に →a から →b の向きとする。
→a と →b の張る平行四辺形の符号付き面積となる。
よって、交換法則は成り立たない。
→a×→b=−→b×→a
また、分配法則が成り立つ。
→c×(→a+→b)=→c×→a+→c×→b
よって
(ax, ay)×(bx, by)=axby−aybx
3次元では次の通り →a と →b に垂直なベクトルとなる。
(ax, ay, az)×(bx, by, bz)=(aybz−azbyazbx−axbzaxby−aybx)
ベクトルを内積すると次元が減ること。
ベクトルを外積すると、あらぬ方向へベクトルが立ち上がること。
「これは不思議だ?」という感覚が五角形の作図へ繋がる。
一次変換
次の方程式、内積の式、ベクトルの式、行列の式は同一である。
{x′=ax+byy′=cx+dy
{x′=(a, b)⋅(x, y)y′=(c, d)⋅(x, y)
(x′y′)=(ac)x+(bd)y
(x′y′)=(abcd)(xy)
いずれもベクトル (x, y) をベクトル (x′, y′) に変換する。
上の式と下の式を見れば、積の順番が分かり易い。
中の式を見ると、正方行列がベクトルの並びであることが理解できる。
この様な、ベクトルに正方行列を掛ける変換を一次変換という。
一次変換の積
行列の積は次の通り。
前側の行列の列数と後側の行列の行数が一致していれば掛け算ができる。
通常は前後を入れ換えると結果が変わるので、一般には交換法則は成り立たない。
(a1b1c1d1)(a2b2c2d2)=(a1a2+b1c2a1b2+b1d2c1a2+d1c2c1b2+d1d2)
おしゃれに書くとたぶんこんな感じになると思うが、自分は2次元と3次元以外の一次変換は使ったことがないので、よく知らない。
(aik)(bkj)=(n∑k=1aikbkj)
すると内積は次の通り。
(ax, ay)⋅(bx, by)=(axay)(bxby)=axbx+ayby
単位行列
対角要素がすべて 1 で他の要素がすべて 0 の正方行列を
単位行列 I という。
I=(1001)
ベクトルに単位行列を掛けることは 1 を掛けることと同じである。
(xy)=(1001)(xy)
逆行列
行列 A に掛けると単位行列 I になる行列を逆行列 A−1 という。
I=AA−1=A−1A
逆行列はベクトルを逆変換する。
(x′y′)=A(xy)
(xy)=A−1(x′y′)
行列 A の逆行列 A−1 は次の通り。
A=(abcd) A−1=1ad−bc(d−b−ca)
行列式
行列 A の行と列を入れ換えた行列を転置行列 tA という。
もいっちょ余因子行列 ˜A という。
A=(abcd) tA=(acbd) ˜A=(d−b−ca)
逆行列は次の通り。
A−1=1|A| ˜A
行列式は次の通り。
|A|=|abcd|=ad−bc
すると外積は次の通り。
(ax, ay)×(bx, by)=|axaybxby|=axby−aybx
3次元では次の通り。
ただし →i, →j, →k は単位ベクトル。
(ax, ay, az)×(bx, by, bz)=|→i→j→kaxayazbxbybz|=|ayazbybz|→i+|azaxbzbx|→j+|axaybxby|→k=(aybz−azbyazbx−axbzaxby−aybx)
ふぅっ。ベクトルはともかく、行列の説明が長かった。
繰り返すが、こんなもんは専門書に詳しい。
うちの子が興味を持ってくれないかな。
実際には、例えばベクトルは x 方向 y 方向の単位ベクトルの合成であることを図を示し、内積・外積はその単位ベクトルで合成した式をひたすら展開して説明した。
説明が下手なのだろう。うちの子は飽きてしまい、結局、正弦定理・余弦定理の説明をすることになってしまった。
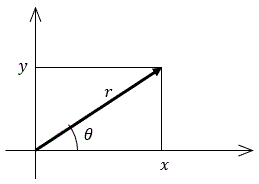
直交座標・極座標
{x=rcosθy=rsinθ のとき (x, y) を直交座標、
(r, θ) を極座標と呼ぶ。
回転行列
大きさ 1 のベクトルを単位ベクトルという。
x 方向の単位ベクトルを →i
すなわち →i=(1, 0) とし、
y 方向の単位ベクトルを →j
すなわち →j=(0, 1) とする。
すると任意のベクトル →r=(x, y) は
→r=x→i+y→j である。
これらを原点の周りに θ 回転する。
→i′=(cosθ, sinθ) となり、
→j′=(−sinθ, cosθ) となる。
また 任意のベクトル →r′=(x′, y′) は
→r′=x→i′+y→j′ となる。
よって (x′, y′)=(xcosθ−ysinθ, xsinθ+ycosθ) である。
(x′y′)=(cosθ−sinθsinθcosθ)(xy)
この様な行列を回転行列という。
回転行列はベクトルを原点の周りに θ 回転する。
加法定理から三角関数の合成まで
原点の周りに α 回転し、さらに β 回転する行列は次の通り。
(cos(α+β)−sin(α+β)sin(α+β)cos(α+β))
=(cosβ−sinβsinβcosβ)(cosα−sinαsinαcosα)
これより加法定理が得られる。
cos(α+β)=cosαcosβ−sinαsinβ
sin(α+β)=sinαcosβ+cosαsinβ
さらに倍角公式が得られる。
cos(2θ)=cos2θ−sin2θ
sin(2θ)=2sinθcosθ
半角公式・和積の公式・積和の公式は略。
asinθ+bcosθ について
→r=(a, b) とする。
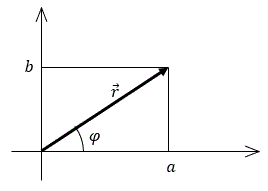 {r=√a2+b2cosφ=arsinφ=br
asinθ+bcosθ
=r(arsinθ+brcosθ)
=r(sinθcosφ+cosθsinφ)
=rsin(θ+φ)
{r=√a2+b2cosφ=arsinφ=br
asinθ+bcosθ
=r(arsinθ+brcosθ)
=r(sinθcosφ+cosθsinφ)
=rsin(θ+φ)
三角関数も復習してみると、こんだけあるんだなぁ~と思った。
指数関数・対数関数・逆関数
y=2x という関数を考える。
x が 1 増えると 2 倍になり、
x が 1 減ると 1/2 倍になる。
x と y を入れ換えた x=2y という関数を考える。
この様な関数を逆関数という。
逆関数はy=x に対称なグラフとなる。
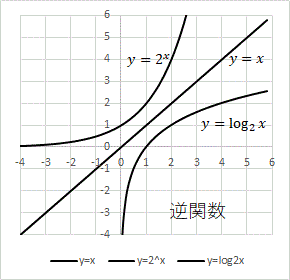
y=ax という関数を指数関数という。
その逆関数 y=logax を対数という。
指数法則と同様に対数法則が成り立つ。
loga1=0
logaa=1
loga(xy)=logax+logay
logaxy=logax−logay
loga(xn)=nlogax
logab=logcblogca
logab=1logba
等差数列・等比数列・漸化式・極限
等差数列
an+1=an+d
等比数列
an+1=ran
等差数列の和
Sn=a+(a+d)+(a+2d)+⋯+(a+(n−1)d)+) Sn=(a+(n−1)d)+⋯+(a+2d)+(a+d)+a2Sn=n{a+a+(n−1)d}
Sn=12n{2a+(n−1)d}
等比数列の和
Sn=a+ar+ar2+⋯+arn−1−) rSn= ar+ar2+⋯+arnSn−rSn=a−arn
Sn=a(1−rn)1−r
微分
関数 y=f(x) 上の2点間の傾き ΔyΔx を、平均の傾きという。
2点を限りなく近づけたとき、接線の傾き dydx という。
接線の傾きを求めることを微分という。
接線の傾きを x の関数で表したものを導関数 dydx=f′(x) という。
dydx=lim
関数の積の微分
\begin{align} y = f(x) g(x) \end{align}
\begin{align} \frac{dy}{dx} & = \lim_{h \to 0} \frac{ f(x+h) g(x+h) - f(x) g(x) }{ h } \\
& = \lim_{h \to 0} {\small \frac{ f(x+h) g(x+h) - f(x) g(x+h) + f(x) g(x+h) - f(x) g(x) }{ h } } \\
& = \lim_{h \to 0} \left\{ \frac{ f(x+h) - f(x) }{ h } g(x+h) + f(x) \frac{ g(x+h) - g(x) }{ h } \right\} \\
& = f'(x) g(x) + f(x) g'(x)
\end{align}
合成関数の微分
\begin{align} y = f(g(x)) \end{align}
\begin{align} \frac{dy}{dx} & = \lim_{h \to 0} \frac{ f(g(x+h)) - f(g(x)) }{ h } \\
& = \lim_{h \to 0} \frac{ f(g(x+h)) - f(g(x)) }{ g(x+h) - g(x) } \frac{ g(x+h) - g(x) }{ h } \\
& = f'(g(x)) g'(x)
\end{align}
べき乗の微分
二項展開の公式より
\begin{align}
( x + h )^n
= {}_{n}\mathrm{\Large C}_{~0} ~ x^n
+ {}_{n}\mathrm{\Large C}_{~1} ~ x^{n-1} h
+ {}_{n}\mathrm{\Large C}_{~2} ~ x^{n-2} h^2
+ \dots \\
+ {}_{n}\mathrm{\Large C}_{~n-2} ~ x^2 h^{n-2}
+ {}_{n}\mathrm{\Large C}_{~n-1} ~ x~h^{n-1}
+ {}_{n}\mathrm{\Large C}_{~n} ~ h^n
\end{align}
ここで
\begin{align} y = x^n \end{align}
\begin{align} \frac{dy}{dx} & = \lim_{h \to 0} \frac{ (x+h)^n - x^n }{ h } \\
& = \lim_{h \to 0} \frac{ ( x^n + n x^{n-1} h + \cdots + h^n ) - x^n }{ h } \\
& = n x^{n-1}
\end{align}
乗数が有理数の場合
\begin{align} y = x^\frac{n}{m} ~~~ y^m = x^n ~~~ m y ^{m-1} dy = n x^{n-1} dx \end{align}
\begin{align} \frac{dy}{dx} = \frac{n x^{n-1}}{m y^{m-1}} = \frac{n}{m} x^{n-1} y^{1-m} = \frac{n}{m} x^{\frac{n}{m}-1}
\end{align}
三角関数の微分
\begin{align} f(\theta) = \sin{\theta} \end{align}
\begin{align} {\Delta}f(\theta) = \sin(\theta+90^\circ){\Delta}\theta \end{align}
\begin{align}
f'(\theta) & = \lim_{{\Delta}\theta \to 0} \frac{{\Delta}f(\theta)}{{\Delta}\theta} \\
& = \sin(\theta+90^\circ) \\
& = \cos{\theta}
\end{align}
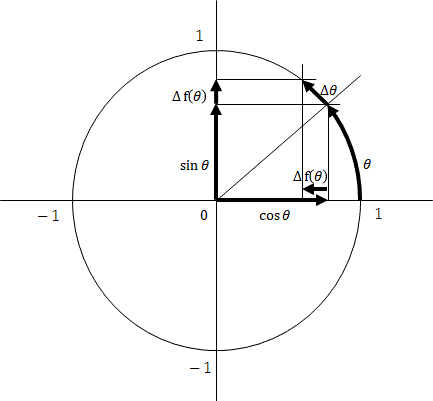 \begin{align} f(\theta) = \cos{\theta} \end{align}
\begin{align} {\Delta}f(\theta) = \cos(\theta+90^\circ){\Delta}\theta \end{align}
\begin{align}
f'(\theta) & = \lim_{{\Delta}\theta \to 0} \frac{{\Delta}f(\theta)}{{\Delta}\theta} \\
& = \cos(\theta+90^\circ) \\
& = -\sin{\theta}
\end{align}
\begin{align} f(\theta) = \cos{\theta} \end{align}
\begin{align} {\Delta}f(\theta) = \cos(\theta+90^\circ){\Delta}\theta \end{align}
\begin{align}
f'(\theta) & = \lim_{{\Delta}\theta \to 0} \frac{{\Delta}f(\theta)}{{\Delta}\theta} \\
& = \cos(\theta+90^\circ) \\
& = -\sin{\theta}
\end{align}
\begin{align} f(\theta) = \tan(\theta) = \frac{\sin{\theta}}{\cos{\theta}}\end{align}
\begin{align}
f'(\theta) & = \frac{\sin^2{\theta}}{\cos^2{\theta}} + \frac{\cos^2{\theta}}{\cos^2{\theta}}
= \tan^2{\theta} + 1 \\
& = \frac{1}{\cos^2{\theta}}
\end{align}
指数関数の微分
y = a^x について考える。
下のグラフは a = 1/2 ,~ 1 ,~ 2 の場合を示している。
これを見ると y 軸と交差する傾きが 1 となる様な a があることが分かる。
この様な a を e で表すことにする。
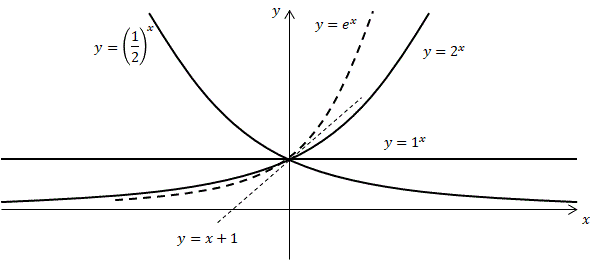 \begin{align} f(x) = e^x \end{align}
\begin{align} f'(x)
= \lim_{h \to 0} \frac{ e^{x+h} - e^x }{ h }
= \lim_{h \to 0} e^x \frac{ e^h - 1 }{ h }
= e^x \lim_{h \to 0} \frac{ e^h - 1 }{ h }
\end{align}
\begin{align} f'(0)
= e^0 \lim_{h \to 0} \frac{ e^h - 1 }{ h }
= 1
\end{align}
\begin{align}
\lim_{h \to 0} \frac{ e^h - 1 }{ h } = 1
\end{align}
\begin{align} f'(x) = e^x \end{align}
この様な
f(x) = e^x のとき f'(x) = e^x となる e を
ネイピア数という。
\begin{align} \lim_{h \to 0} \frac{ e^h - 1 }{ h } = 1 \end{align}
\begin{align} \lim_{h \to 0} \left\{ \frac{ e^h - 1 }{ h } = 1 \right\} \end{align}
\begin{align} \lim_{h \to 0} \left\{ e^h - 1 = h \right\} \end{align}
\begin{align} \lim_{h \to 0} \left\{ e^h = 1 + h \right\} \end{align}
\begin{align} \lim_{h \to 0} \left\{ e = ( 1 + h )^{1/h} \right\} \end{align}
\begin{align} e = \lim_{h \to 0} ( 1 + h )^{1/h} \end{align}
\begin{align} e = \lim_{k \to \infty} \left( 1 + \frac{1}{k} \right)^k \end{align}
\begin{align} e^x = \lim_{k \to \infty} \left( 1 + \frac{x}{k} \right)^k \end{align}
これを計算すると e = 2.718281828459045 \cdots となる。
\begin{align} f(x) = e^x \end{align}
\begin{align} f'(x)
= \lim_{h \to 0} \frac{ e^{x+h} - e^x }{ h }
= \lim_{h \to 0} e^x \frac{ e^h - 1 }{ h }
= e^x \lim_{h \to 0} \frac{ e^h - 1 }{ h }
\end{align}
\begin{align} f'(0)
= e^0 \lim_{h \to 0} \frac{ e^h - 1 }{ h }
= 1
\end{align}
\begin{align}
\lim_{h \to 0} \frac{ e^h - 1 }{ h } = 1
\end{align}
\begin{align} f'(x) = e^x \end{align}
この様な
f(x) = e^x のとき f'(x) = e^x となる e を
ネイピア数という。
\begin{align} \lim_{h \to 0} \frac{ e^h - 1 }{ h } = 1 \end{align}
\begin{align} \lim_{h \to 0} \left\{ \frac{ e^h - 1 }{ h } = 1 \right\} \end{align}
\begin{align} \lim_{h \to 0} \left\{ e^h - 1 = h \right\} \end{align}
\begin{align} \lim_{h \to 0} \left\{ e^h = 1 + h \right\} \end{align}
\begin{align} \lim_{h \to 0} \left\{ e = ( 1 + h )^{1/h} \right\} \end{align}
\begin{align} e = \lim_{h \to 0} ( 1 + h )^{1/h} \end{align}
\begin{align} e = \lim_{k \to \infty} \left( 1 + \frac{1}{k} \right)^k \end{align}
\begin{align} e^x = \lim_{k \to \infty} \left( 1 + \frac{x}{k} \right)^k \end{align}
これを計算すると e = 2.718281828459045 \cdots となる。
底が e の対数 \log_{e}x を自然対数と呼び \ln x と表す。
対数関数の微分
\begin{align} y = \log{x} \end{align}
\begin{align} x = e^y \end{align}
\begin{align} \frac{dx}{dy} = e^y \end{align}
\begin{align} \frac{dy}{dx} = \frac{1}{e^y} = \frac{1}{x} \end{align}
さて、もう一度。
\begin{align} f(x) = \log{x} ~~~ (x>0) \end{align}
\begin{align} f'(x) = \frac{1}{x} \end{align}
\begin{align} f(x) = \log(-x) ~~~ (x<0) \end{align}
\begin{align} f'(x) = \frac{-1}{-x} = \frac{1}{x} \end{align}
したがって
\begin{align} f(x) = \log|x| \end{align}
\begin{align} f'(x) = \frac{1}{x} \end{align}
微分・積分
微分は傾きを求めること。
積分は面積を求めること。
\begin{align} \int_{x_1}^{x_2} f(x) dx = \lim_{n \to \infty} \left\{ \frac{x_2 - x_1}{n} \sum_{k = 1}^{n} f \left( x_1 + \frac{x_2 - x_1}{n} k \right) \right\} \end{align}
F'(x) = f(x) のとき定積分は次の通り。
\begin{align} \int_{x_1}^{x_2} f(x) dx = \left[ F(x) \right]_{x_1}^{x_2} = F(x_2)-F(x_1) \end{align}
F'(x) = f(x) のとき不定積分は次の通り。
\begin{align} \int f(x) dx = F(x) + C \end{align}
高校数学に於いて、積分とは導関数の原始関数を求めることである。
原始関数を覚えてないと解けない。
ラグランジュ補間
2点を通る1次式を求めることができる。
3点を通る2次式を求めることができる。
一般に n+1 点を通る n 次式を求めることができる。
連立方程式を立て係数について解く。
多元多次方程式にも適用できる。
補間法としては点が多いと無理なカーブになりやすいのが弱点。
最小自乗法
n+1 より多い点に対し y 方向の残差の自乗の合計が最小となる n 次式を求めることができる。
正規方程式を得て連立方程式として解く。
多元多次方程式にも適用できる。
テイラー展開
f(x) について x=x_0 の時の値を得ることができる。
f'(x) から x=x_0 の時の傾きを得て接線を求めることができる。
f''(x) から x=x_0 の時の曲率を得て…
無限に微分可能な f(x) についてテイラー級数を考えることができる。
\begin{align} f(x) = f(x_0) + f'(x_0) (x - x_0) + \frac{f''(x_0)}{2} (x - x_0)^2 + \\
\cdots + \frac{f^{(n)}(x_0)}{n!} (x - x_0)^n + \cdots \end{align}
無限に展開すれば元の関数と一致すると考えられる。
高次の項を無視しても x=x_0 付近の近似式として使える。
マクローリン展開(べき級数展開)
同様に x=0 付近についてマクローリン級数(べき級数)を考えることができる。
\begin{align} f(x) = f(0) + f'(0) x + \frac{f''(0)}{2} x^2 + \\
\cdots + \frac{f^{(n)}(0)}{n!} x^n + \cdots \end{align}
無限に展開すれば元の関数と一致すると考えられる。
フーリエ変換
離散データのフーリエ変換
等間隔離散データの高速フーリエ変換
省略
e^x の展開・ e の展開
\begin{align} f(x) = e^x = a_0 + a_1 x + a_2 x^2 + \cdots + a_n x^n + \cdots \end{align}
\begin{align} f(0) = e^0 = 1 ~~~ \mbox{∴} a_0 = 1 \end{align}
\begin{align} f'(x) = e^x = a_1 + 2 a_2 x + 3 a_3 x^2 + \cdots + n a_n x^{n-1} + \cdots \end{align}
\begin{align} f'(0) = e^0 = 1 ~~~ \mbox{∴} a_1 = 1 \end{align}
\begin{align} f''(x) = e^x = {\small 2 \cdot 1 a_2 + 3 \cdot 2 a_3 x + 4 \cdot 3 a_3 x^2 + \cdots + n (n-1) a_n x^{n-2} + \cdots } \end{align}
\begin{align} f''(0) = e^0 = 1 ~~~ \mbox{∴} a_2 = \frac{1}{2 \cdot 1} \end{align}
以下同様より
\begin{align} e^x = \frac{x^0}{0!} + \frac{x^1}{1!} + \frac{x^2}{2!} + \frac{x^3}{3!} + \cdots + \frac{x^n}{n!} + \cdots \end{align}
x = 1 を代入
\begin{align} e = \frac{1}{0!} + \frac{1}{1!} + \frac{1}{2!} + \frac{1}{3!} + \cdots + \frac{1}{n!} + \cdots \end{align}
\sin{x} の展開
\begin{align} f(x) = \sin{x} = a_0 + a_1 x + a_2 x^2 + \cdots \end{align}
\begin{align} f(0) = \sin{0} = 0 ~~~ \mbox{∴} a_0 = 0 \end{align}
\begin{align} f'(x) = \cos{x} = a_1 + 2 a_2 x + 3 a_3 x^2 + \cdots \end{align}
\begin{align} f'(0) = \cos{0} = 1 ~~~ \mbox{∴} a_1 = 1 \end{align}
\begin{align} f''(x) = - \sin{x} = {\small 2 \cdot 1 a_2 + 3 \cdot 2 a_3 x + 4 \cdot 3 a_3 x^2 + \cdots } \end{align}
\begin{align} f''(0) = - \sin{0} = 0 ~~~ \mbox{∴} a_2 = 0 \end{align}
\begin{align} f'''(x) = - \cos{x} = {\small 3 \cdot 2 \cdot 1 a_3 + 4 \cdot 3 \cdot 2 a_4 x + 5 \cdot 4 \cdot 3 a_5 x^2 + \cdots } \end{align}
\begin{align} f'''(0) = - \cos{0} = - 1 ~~~ \mbox{∴} a_3 = - \frac{1}{3 \cdot 2 \cdot 1} \end{align}
以下同様より
\begin{align} \sin{x} = 0 + \frac{x^1}{1!} - 0 - \frac{x^3}{3!} + 0 + \frac{x^5}{5!} - 0 - \frac{x^7}{7!} + \cdots \end{align}
\cos{x} の展開
\begin{align} f(x) = \cos{x} = a_0 + a_1 x + a_2 x^2 + \cdots \end{align}
\begin{align} f(0) = \cos{0} = 1 ~~~ \mbox{∴} a_0 = 1 \end{align}
\begin{align} f'(x) = - \sin{x} = a_1 + 2 a_2 x + 3 a_3 x^2 + \cdots \end{align}
\begin{align} f'(0) = - \sin{0} = 0 ~~~ \mbox{∴} a_1 = 0 \end{align}
\begin{align} f''(x) = - \cos{x} = {\small 2 \cdot 1 a_2 + 3 \cdot 2 a_3 x + 4 \cdot 3 a_3 x^2 + \cdots } \end{align}
\begin{align} f''(0) = - \cos{0} = 0 ~~~ \mbox{∴} a_2 = \frac{1}{2 \cdot 1} \end{align}
\begin{align} f'''(x) = \sin{x} = {\small 3 \cdot 2 \cdot 1 a_3 + 4 \cdot 3 \cdot 2 a_4 x + 5 \cdot 4 \cdot 3 a_5 x^2 + \cdots } \end{align}
\begin{align} f'''(0) = \sin{0} = - 1 ~~~ \mbox{∴} a_3 = 0 \end{align}
以下同様より
\begin{align} \cos{x} = \frac{x^0}{0!} - 0 - \frac{x^2}{2!} + 0 + \frac{x^4}{4!} - 0 - \frac{x^6}{6!} + \cdots \end{align}
\arctan{x} の展開・ \pi の展開
等比数列の和の公式より
\begin{align} S_n = 1 - x^2 + x^4 - x^6 + \cdots + x^{2 (n-1)}= \frac{ 1 \{ 1 - ( - x^2)^n \} }{ 1 - (-x^2) } \end{align}
|-x^2| < 1 のとき
\begin{align} \lim_{n \to \infty} S_n = 1 - x^2 + x^4 - x^6 + \cdots = \frac{ 1 }{ 1 + x^2 } \end{align}
ここで
\begin{align} y = \arctan{x} \end{align}
\begin{align} x = \tan{y} \end{align}
\begin{align} \frac{dx}{dy} = 1 + \tan^2{y} \end{align}
\begin{align} \frac{dy}{dx} & = \frac{1}{1 + \tan^2{y}} = \frac{1}{1 + x^2} \\
& = 1 - x^2 + x^4 - x^6 + \cdots \end{align}
\begin{align} y = x - \frac{x^3}{3} + \frac{x^5}{5} - \frac{x^7}{7} + \cdots \end{align}
この等式は -1 < x < 1 で y = \arctan{x} と一致するが、
その延長でも(範囲を限らず)一致していると考えられる。
グレゴリー級数
\begin{align} \arctan{x} = x - \frac{x^3}{3} + \frac{x^5}{5} - \frac{x^7}{7} + \cdots \end{align}
\tan{\frac{\pi}{4}} = 1 を代入。
ライプニッツの公式
\begin{align} \frac{\pi}{4} = 1 - \frac{1}{3} + \frac{1}{5} - \frac{1}{7} + \cdots \end{align}
x が小さい方が収束が早い。 \tan{\frac{\pi}{6}} = \frac{1}{\sqrt{3}} を代入。
\begin{align} \pi = \sqrt{12} \left( 1 - \frac{1}{3 \cdot 3} + \frac{1}{5 \cdot 3^2 } - \frac{1}{7 \cdot 3^3 } + \cdots \right) \end{align}
他に
\begin{align} \frac{\pi}{4} = \arctan{\frac{1}{2}} + \arctan{\frac{1}{3}} \end{align}
\begin{align} \frac{\pi}{4} = 4 \arctan{\frac{1}{5}} + \arctan{\frac{1}{239}} \end{align}
自然数・整数・有理数(分数)・無理数・複素数(虚数)
虚数: i = \sqrt{-1}
複素数: z = a + b i
ガウス平面:実軸と虚軸の直交座標
\begin{align}
1 \times i & = i \\
i \times i & = -1 \\
-1 \times i & = -i \\
-i \times i & = 1
\end{align}
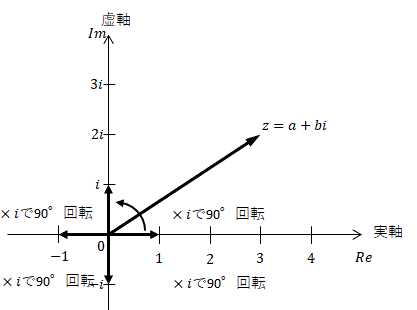 i を乗ずるとガウス平面上で 90^\circ 回転する。
i を乗ずるとガウス平面上で 90^\circ 回転する。
複素数の加法・乗法
複素数の極形式
\begin{align} z = r ( \cos{\theta} + i \sin{\theta} ) \end{align}
ド・モアブルの定理
\begin{align}
z_1 \times z_2 & = a ( \cos{\alpha} + i \sin{\alpha} ) \times b ( \cos{\beta} + i \sin{\beta} ) \\
& = a b \{ ( \cos{\alpha} \cos{\beta} - \sin{\alpha} \sin{\beta} ) + i ( \sin{\alpha} \cos{\beta} + \cos{\alpha} \sin{\beta} ) \} \\
& = a b \{ \cos(\alpha + \beta) + i \sin(\alpha + \beta) \}
\end{align}
従来の定義だと虚数の扱いが不明なので、次の通り再定義する。
\begin{align}
e^x & = \frac{x^0}{0!} + \frac{x^1}{1!} + \frac{x^2}{2!} + \frac{x^3}{3!} + \frac{x^4}{4!} + \frac{x^5}{5!} + \frac{x^6}{6!} + \frac{x^7}{7!} + \cdots \\
\cos{x} & = \frac{x^0}{0!} - 0 - \frac{x^2}{2!} + 0 + \frac{x^4}{4!} - 0 - \frac{x^6}{6!} + 0 + \cdots \\
\sin{x} & = 0 + \frac{x^1}{1!} - 0 - \frac{x^3}{3!} + 0 + \frac{x^5}{5!} - 0 - \frac{x^7}{7!} + \cdots
\end{align}
これより
\begin{align}
e^{i \theta} & = \frac{\theta^0}{0!} + i \frac{\theta^1}{1!} - \frac{\theta^2}{2!} - i \frac{\theta^3}{3!} + \frac{\theta^4}{4!} + i \frac{\theta^5}{5!} - \frac{\theta^6}{6!} - i \frac{\theta^7}{7!} + \cdots \\
\cos{\theta} & = \frac{\theta^0}{0!} - 0 - \frac{\theta^2}{2!} + 0 + \frac{\theta^4}{4!} - 0 - \frac{\theta^6}{6!} + 0 + \cdots \\
i \sin{\theta} & = 0 + i \frac{\theta^1}{1!} - 0 - i \frac{\theta^3}{3!} + 0 + i \frac{\theta^5}{5!} - 0 - i \frac{\theta^7}{7!} + \cdots
\end{align}
以上よりオイラーの公式が得られる
\begin{align} e^{i \theta} = \cos{\theta} + i \sin{\theta} \end{align}
極形式で一般化する
\begin{align} r e^{i \theta} = r ( \cos{\theta} + i \sin{\theta} ) \end{align}
r = 1 ,~ \theta = \pi を代入するとオイラーの等式(人類の至宝)が得られる
\begin{align} e^{i \pi} +1 = 0 \end{align}
正五角形の作図
z^5=1 の解は
z = \cos{\theta} + i \sin{\theta} とすると
5 \theta = 0 ,~ \pm 2 \pi ,~ \pm 4 \pi である事は自明であるが
具体的な値を求める。
z^5 - 1 = 0 を因数分解すると次の通り。
\begin{align} z^5 - 1 = ( z - 1 )( z^4 + z^3 + z^2 + z + 1 ) = 0 \end{align}
z \ne 1 のとき
両辺を z-1 で除して
\begin{align} z^4 + z^3 + z^2 + z + 1 = 0 \end{align}
両辺を z^2 で除して
\begin{align} z^2 + z + 1 + \frac{1}{z} + \frac{1}{z^2} = 0 \end{align}
t = z + \frac{1}{z} とすると t^2 = z^2 + 2 + \frac{1}{z^2} なので
\begin{align}
z^2 + z + 1 + \frac{1}{z} + \frac{1}{z^2}
& = z^2 + 2 + \frac{1}{z^2} + z + \frac{1}{z} - 1 \\
& = t^2 + t - 1
= 0
\end{align}
より
\begin{align} t = \frac{ - 1 \pm \sqrt{5} }{2} \end{align}
ここで
\begin{align}
\frac{1}{z} & = z^{-1} = (e^{i \theta})^{-1} = e^{-i\theta} \\
& = \cos(-\theta) + i \sin(-\theta) = \cos{\theta} - i \sin{\theta}
\end{align}
なので
\begin{align}
t & = z + \frac{1}{z} \\
& = ( \cos{\theta} + i \sin{\theta} ) + ( \cos{\theta} - i \sin{\theta} ) \\
& = 2 \cos{\theta} = \frac{ - 1 \pm \sqrt{5} }{2}
\end{align}
\cos{\theta} = \frac{ - 1 + \sqrt{5} }{4} のとき
\begin{align}
\sin{\theta} = \pm \sqrt{1 - \cos^2{\theta}} = \sqrt{1-\left(\frac{-1+\sqrt{5}}{4}\right)^2} = \frac{\pm\sqrt{10 + 2 \sqrt{5}}}{4}
\end{align}
\cos{\theta} = \frac{ - 1 - \sqrt{5} }{4} のとき
\begin{align}
\sin{\theta} = \pm \sqrt{1 - \cos^2{\theta}} = \sqrt{1-\left(\frac{-1-\sqrt{5}}{4}\right)^2} = \frac{\pm\sqrt{10 - 2 \sqrt{5}}}{4}
\end{align}
以上より
\begin{align}
z = \cos{\theta} + i \sin{\theta}
= \left\{
\begin{array}{cl}
1 && ( \theta = 0 ) \\
\frac{ - 1 + \sqrt{5} }{4} \pm \frac{\sqrt{10 + 2 \sqrt{5}}}{4} i && ( \theta = \pm \frac{2 \pi}{5} ) \\
\frac{ - 1 - \sqrt{5} }{4} \pm \frac{\sqrt{10 - 2 \sqrt{5}}}{4} i && ( \theta = \pm \frac{4 \pi}{5} )
\end{array}
\right.
\end{align}
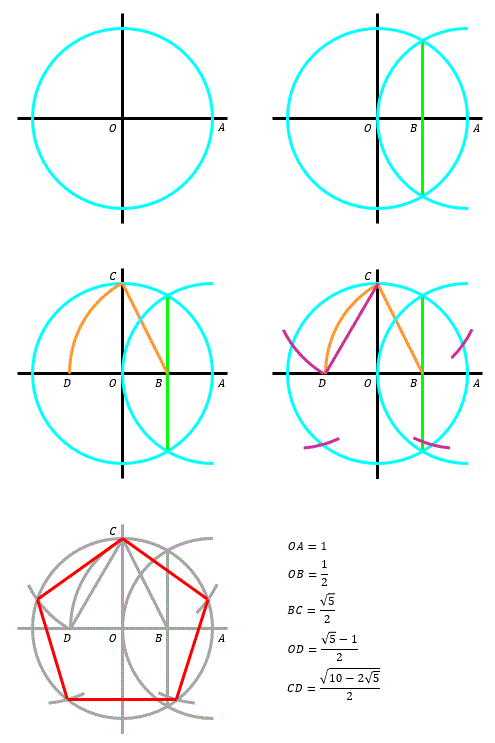
|  Genta Labo
Genta Labo
 Genta Labo
Genta Labo










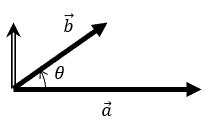





![]() ECナビでポインと Yahoo 楽天
ECナビでポインと Yahoo 楽天 LINEがデータ消費ゼロで月額500円~!
![]() 海外旅行保険が無料! 海外ホテル
海外旅行保険が無料! 海外ホテル