コラッツ問題を考えてみた

prev | 1 | 2 | 3 | 4 | 5 | 6 | 7 | next

初版公開2023年10月28日

コラッツ問題を考えてみた

SNSには「踊ってみた」という動画が溢れているが、これにタイトルを真似た。
最初に断っておくが、本稿は筆者のメモであり、何等の証明にも至っていない。
拙い考察であるが、御笑読いただければ幸いである。
Abstractに代えて、本稿の章立てを掲載する。

コラッツ問題の紹介
- コラッツ問題
- 試行
- 知っておいた方がいいこと
等価な操作
- 桁下げ有り操作
- 桁下げ無し操作
- コラッツ掃出し
合流（遡りでは分岐）
- コラッツ兄弟
- コラッツ双子
- 遡り展開
証明すべき課題
- 奇数の周期表
- 漸化式の一般項
- コラッツ掃寄せ
- コラッツ縞
雑多なこと（メモ）

コラッツ問題

ヨビノリの動画でコラッツ問題を知った。

整数 \(x_0\) について \begin{align} x_{i+1}=\left\{ \begin{array}{ll} x_i/2 &（x_i が偶数）\\ 3x_i+1 &（x_i が奇数） \end{array} \right. \end{align} （以下「コラッツ変換」と呼称する）

任意の正の整数 \(x_0\) について、この操作の有限の反復で \(1\) に到達する、というのがコラッツ予想で、その真偽を証明することがコラッツ問題である。
この問題の誕生は1930年代、広く知られたのは1950年とされており、未解決問題となっている。つまり、どんな正の整数から始めても必ず \(1\) になんじゃね？状態のままということ。

試行

次の図は \(1\) ～ \(16\) についてコラッツ変換の試行である。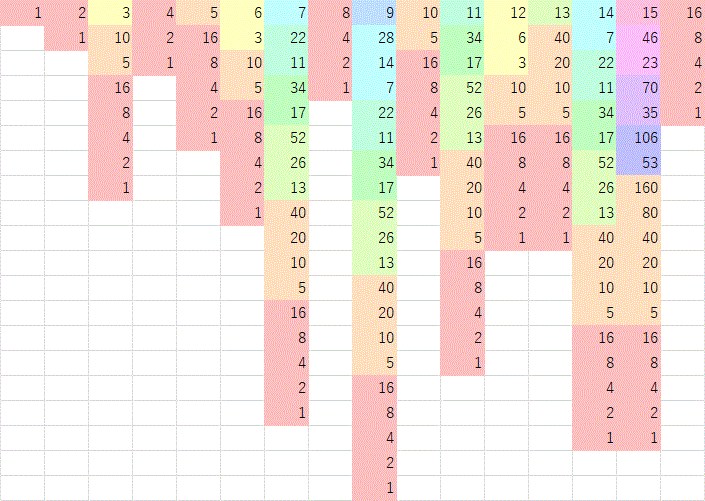
1行目が初期値で、縦方向に変換結果を示した。

図1：1～16のコラッツ変換の結果

奇数で終わる公比 \(1/2\) の等比数列（初項が奇数で公比 \(2\) の等比数列の逆順）で色分けし、同じ数列は同色に塗り分けた。
奇数の変遷に着目すればよい、ということが判る。

\(1\) の数列は \(1\) に到達している。
\(3\) の数列は \(5\) の数列に移る、
\(5\) の数列は \(1\) の数列に移る、\(1\) の数列は確認済。
\(9\) の数列は \(7\) の数列に移る、
\(7\) の数列は \(11\) の数列に移る、
\(11\) の数列は \(17\) の数列に移る、
\(17\) の数列は \(13\) の数列に移る、
\(13\) の数列は \(5\) の数列に移る、\(5\) の数列は確認済。
･･･
確認済の数列に移ることを確認した時点で当該数列も確認済となる。

知っておいた方がいいこと

筆者は、先達の研究を何等調査すること無く、いきなり問題に取り組んでしまった。
数学の論文の探し方がよく分からない。
今もろくに何も調べていないが、これは褒められた態度とは言えない。
最低限、知っておいた方がいいことを、列挙しておく。

\(1\) から辿ると、無数に分岐する樹状構造になる。

定義域を（正の整数に限らないで）整数全体に拡張すると \(1, 0, -1, -5, -17\) は循環する。

\(x\) が奇数の場合 \(3x+1\) は必ず偶数なので、次の様にショートカットできる。

\begin{align} x_{i+1}=\left\{ \begin{array}{ll} \frac{x_i}{2} &（x_i が偶数）\\ \frac{3x_i+1}{2} &（x_i が奇数） \end{array} \right. \end{align}

\(x\) が奇数なら \(-1\) となり偶数なら \(+1\) となる関数 \(\mbox{k}(x)\) を導入する。
\(\frac{1+k(x)}{2}\) は \(x\) が偶数なら \(1\) となり奇数なら \(0\) となる。
\(\frac{1-k(x)}{2}\) は \(x\) が奇数なら \(1\) となり偶数なら \(0\) となる。
これを用いて1行の式で表すことができる。

\begin{align} x_{i+1} = \frac{x_i}{2} \cdot \frac{1+k(x_i)}{2} + \frac{3x_i+1}{2} \cdot \frac{1-k(x_i)}{2} \end{align}

\(\mbox{k}(x)\) を \(\mbox{cos}({\pi}x)\) に置き換えて、定義域を実数に拡張できる。
あるいは \(\mbox{cos}({\pi}x)+j~\mbox{sin}({\pi}x)\) に置き換えて、定義域を複素数に拡張できる。
複素平面上で特異点の分布はジュリア集合を描くらしい。
ここで言う特異点とは、そこを初期値にすると発散しない点のことであり、すべての正の整数は \(1\) に収束する（と予想される）ので、ここで描かれるジュリア集合は、実軸の正の整数はすべて特異点となるのだろう。

この問題を桁下げ無し操作（後述）で扱うと常に増分となるが、桁数を増やしていくに従って、分解能が上がると共に \(+1\) の効果が小さくなって、実数の指数関数 \(x_i=x_0(3/2)^i\) に近似する。これを考え始めると、整数と実数の違いが分からなくなる。

なお、ほとんど全ての正の整数は元の数より小さくなる（すなわち \(1\) になる）ことが、既に、確率と偏微分方程式の考え方を用いて証明されている。

因数分解（筆者の動機）

高校数学は、実数の \(x^n=1\) の解に始まり、複素数の \(z^n=1\) の解に至る。これにより正五角形の作図ができるようになるので、自分の中では正五角形作図の物語と名付けている。クライマックスはオイラーの等式 \(e^{j\pi}=-1\) ということになろうか。涙あふれる（数学の宿題のせい？）感動の一大スペクタクルである。

\(x^2-1=0\) は解を持つが、\(x^2+1=0\) は解を持たない。 \(x^2-a=0\) で \(a\) を変化させていくと \(a=0\) でプツンと途切れてしまう。しかし、裏の世界で連続的に繋がっているに違いないという確信と、 \(n\) 次方程式は \(n\) 個の解が必要という要求から、虚数 \(\sqrt{-1}\) が誕生したと思われる。このような関連から、複素平面上のフラクタル図形を整数に限って扱う場合は、因数分解が有効な手段ではないかという期待を筆者は持っている。

さて、因数分解である。 \begin{align} x^n=1 \end{align} は \(x=1\) の解を持つことは自明なので \(1\) を移項した \begin{align} x^n-1=0 \end{align} の左辺は \(x-1\) で因数分解できる。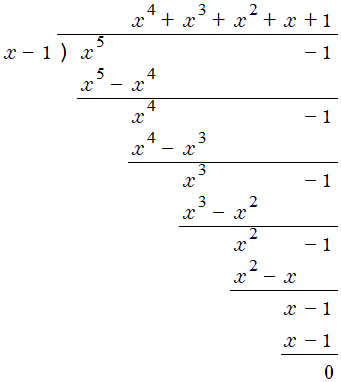

つまり \begin{align} \begin{array}{l} x^1-1=(x-1)(x^0) \\ x^2-1=(x-1)(x^1+x^0) \\ x^3-1=(x-1)(x^2+x^1+x^0) \\ x^4-1=(x-1)(x^3+x^2+x^1+x^0) \\ x^5-1=(x-1)(x^4+x^3+x^2+x^1+x^0) \\ \cdots \end{array} \end{align} これに \(x=4\) を代入すると \begin{align} \begin{array}{l} 4^1-1=(4-1)(4^0) \\ 4^2-1=(4-1)(4^1+4^0) \\ 4^3-1=(4-1)(4^2+4^1+4^0) \\ 4^4-1=(4-1)(4^3+4^2+4^1+4^0) \\ 4^5-1=(4-1)(4^4+4^3+4^2+4^1+4^0) \\ \cdots \end{array} \end{align} すなわち \begin{align} \begin{array}{l} 4^1-1=3(4^0) \\ 4^2-1=3(4^1+4^0) \\ 4^3-1=3(4^2+4^1+4^0) \\ 4^4-1=3(4^3+4^2+4^1+4^0) \\ 4^5-1=3(4^4+4^3+4^2+4^1+4^0) \\ \cdots \end{array} \end{align} \(4^n-1\) は \(3\) で割り切れ、\(4\) のべき級数になる。 \(x=4\) に限らず \(x=3n+1\) を代入すれば、\(3\) で割り切れ、べき級数になる。
蛇足だが \(x\) のべき級数は \(x\) 進数で表記すると \(1\cdots1_{(x)}\) である。コラッツ問題を知った直後は何の関心も持たなかったが、取り組んでみる気になったのは、\(1\) の連続という概念に急に捕らわれてしまったためである。ちなみに \(2\) 進数で \(-1\) の \(2\) の補数は \(1\) の連続だが、ここではあまり関係がない。

prev | 1 | 2 | 3 | 4 | 5 | 6 | 7 | next

Gポイントポイ活　 Amazon Yahoo 楽天

無料ホームページ楽天モバイル[UNLIMITが今なら1円] 海外格安航空券海外旅行保険が無料！