prev |  1 |  2 |  3 |  4 |  5 |  6  |  7 |  next

コラッツ縞

  さてもう一度、\(31\) から \(91\) である。 \(31\)は、末尾の連続1が \(5\) 個、上位の値が \(0\) であり、反同期である。 コラッツ掃出しは、末尾の1がひとつ減り、上位の値が \(u_{i+1}=3u_i+1\) になる。 区切りの0の上位の2bit（即ち上位の値の末尾2bit）を橙着色した。 \(121\) の末尾に注意。 今までは末尾の桁が上がり、新たなコラッツ掃出しとしていたところを、お構いなしに連続で塗りつぶし、\(31\)〜\(91\) を連続のものとして扱っている。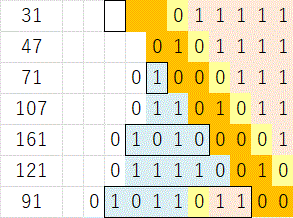

図20：\(31\)〜\(91\)の変遷

\(u_{i+1}=3u_i+1\) は末尾2bitが \(00_{(2)},01_{(2)}\) の交互または \(10_{(2)},11_{(2)}\) の交互になる。 この関係は（上位の値の偶奇と末尾の連続1の数の偶奇が）反同期の場合はコラッツ掃出しが終了するひとつ先（図では \(5\) 回 \(+1\) 回）まで継続して進行する。

  先述の9進数について振り返ると、 \(u_{i+1}=3u_i+1\) に対し上位の値の末尾2bitは、 そのさらに上位への繰上げが \(00_{(2)}\) のときは \(0\) で、 \(01_{(2)}\) のときは \(1\) なので、 上位の値の末尾2bitより上位の値は \(uu_{i+1}=3uu_i\) と \(uu_{i+1}=3uu_i+1\) の交互になる。 その結果 \(uu_{i+2}=9uu_i+1\) となり、図の枠で囲った部分の値は \(\{0,1,10,91\}\) 即ち \(\{0_{(9)},1_{(9)},11_{(9)},111_{(9)}\}\) となる、 のだった。

で、それが何？ 上位の値の上位部分が \(uu_{i+2}=9uu_i+1\) で進行すると何か嬉しいの？ 上位の値が \(u_{i+1}=3u_i+1\) で進行するでいいじゃん。 そうですね、何も嬉しくありません。 2進で末尾の連続1をひとつづつ減らしながら、3進で上位の連続1がひとつづつ増えていく、の方が解りやすい。 上位の値の進行が、反同期の場合はコラッツ掃出し終了のひとつ先（コラッツ双子の合流部）まで継続するということ、の気付きに繋がっただけです。

  と言う訳で、反同期の場合は（コラッツ掃出し単位のショートカットでなく）ひとつ先のコラッツ双子の合流部までをショートカットすることを考える。 コラッツ双子の合流部まで連続で塗りつぶす感じで、上位の値の末尾2bitを着色した。

図21：初期値 \(27\) からの変遷

縞模様が現れた。 斜め縞なのは、本稿ではコラッツ変換を \(x_{i+1}=(3x_i+1)/2\) としている為である。 桁下げ無し操作なので \(/2\) は不要だが、紙幅が足りないので（最終定理か？意味が違う！）この様にしている。 で \(/2\) しなければ縦縞である。 いずれにせよ、反同期の場合はコラッツ掃出しのひとつ先まで連続で進行することは図より明らかである。

縞模様は互いにオーバーラップしており、オーバラップが一般に成立することは（詳細は省くが）図より明らか。 よって、ひとつの縞の終端まで計算すれば、次の縞の計算を開始できる。 ただし、\(00_{(2)},01_{(2)}\) では \(00_{(2)}\) まで計算すると次の縞の計算を開始できるが、 \(10_{(2)},11_{(2)}\) では \(10_{(2)}\) まで計算しようが \(11_{(2)}\) まで計算しようが、前述のコラッツ掃出しの終端までスキップとあまり変わらない。 \(10_{(2)},11_{(2)}\) についてはひとまず保留し、\(00_{(2)},01_{(2)}\) の場合だけ、反同期であればコラッツ掃出しのひとつ先までスキップする。 末尾が必ず \(00_{(2)}\) になるので \(/4\) する。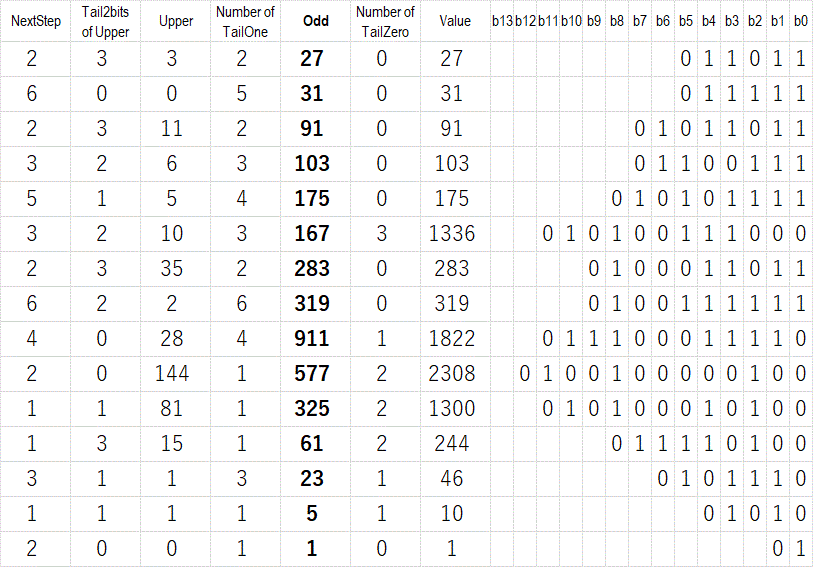

図22：初期値 \(27\) からの変遷 （ダウンロードはこちら）

図18より図22の方がちょびっとだけ短くなった。

  保留した上位の値の末尾2bitが \(10_{(2)},11_{(2)}\) の場合については、何通りかの方法が考えられる。

(1)

保留したまま。つまりコラッツ掃出しの終端までをスキップする方法。

(2)

反同期の場合は、コラッツ掃出しの終端のひとつ先までをスキップする方法。

(3)

この場合、末尾が \(10_{(2)}\) となるから、\(/2\) して \((3x+1)/2\) して、さらにもうひとつ先まで進める方法。

(4)

むしろひとつ戻って、末尾 \(11_{(2)}\) まで、すなわち今の縞がどこまで続くかよりも次の縞がどこから始まるかを辿る方法。

どの方法が証明に辿り着くのか（あるいはどれも辿り着かないのか）判らない。 でもまぁいっか。膨張して収縮、もはや雹モデルではない。 収縮に転じる条件は何だろう？

prev |  1 |  2 |  3 |  4 |  5 |  6  |  7 |  next