prev |  1 |  2 |  3 |  4  |  5 |  6 |  7 |  next

奇数の周期表

  例えば、4bitまでの奇数が全て収束するなら6bitまでの奇数も全て収束する、といった関係が 一般に成立していれば、数学的帰納法で問題は決着する。

コラッツ兄弟に限れば、このような関係は成立する。 下図の5〜6bit奇数の着色部は3〜4bit奇数のコラッツ兄弟であり、 4bitまでの奇数が全て収束するなら、収束する。

図8：奇数の周期表 3〜4bit奇数（赤字）のコラッツ兄弟
すなわち末尾 \(101_{(2)}\)を着色

末尾 \(001_{(2)}\) 末尾 \(011_{(2)}\) も見てみる。 赤字が行き先であり、規則的である。 いづれも元の数より小さくなっており、 世代の最小値の \(17\) と \(19\) は下位の世代へ行くので、 4bitまでの奇数が全て収束するなら、収束する。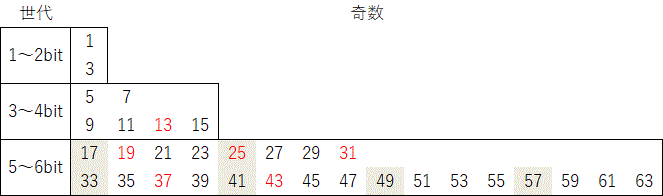

図9：奇数の周期表 末尾 \(001_{(2)}\)を着色 赤字が行き先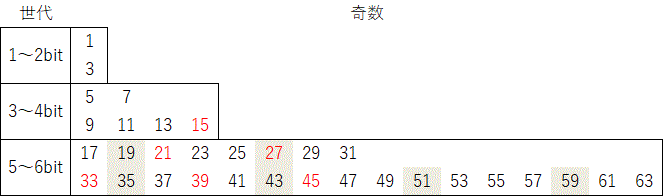

図10：奇数の周期表 末尾 \(011_{(2)}\)を着色 赤字が行き先

最後に末尾 \(111_{(2)}\) を見てみる。 赤字が行き先であり、規則的である。 いづれも元の数より大きくなっている。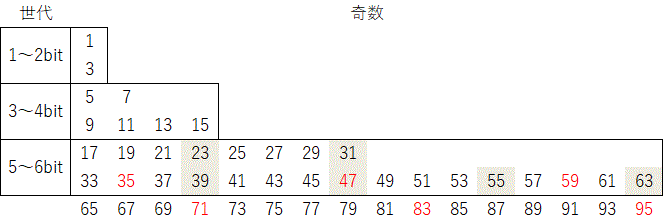

図11：奇数の周期表 末尾 \(111_{(2)}\)を着色 赤字が行き先

厄介なのが \(2^n-1\)すなわち2進で \(\mbox{all}~1_{(2)}\) の数である。 末尾の1が続くので、コラッツ掃出しで初期のbit長よりも膨張して、上位の世代へ行ってしまう。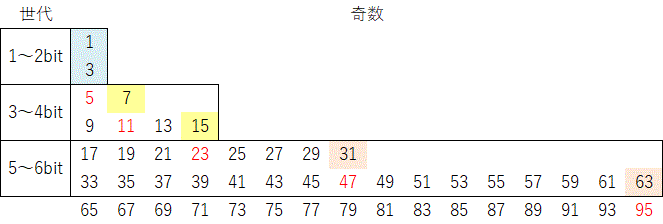

図12：奇数の周期表 \(\mbox{all}~1_{(2)}\) を着色 赤字が行き先

この周期表では丁度真下へ1コマ移動する。ここで \(\{1,3\},\{7,15\},\{31,63\},\cdots\) はそれぞれコラッツ双子である。 双子は一方が収束するなら他方も収束するので、どちらかだけを確認できればよい。

ひとつ下位に目を移してみると、 \(7\) はしばらく彷徨った末に \(3\) のコラッツ兄弟である \(13\) へ辿り着く。 \(15\) はしばらく彷徨った末に \(3\) のコラッツ兄弟である \(53\) へ辿り着く。

図13：奇数の周期表 \(7\) と \(15\) の軌跡を着色

同様に \(31,63\) は上位の世代をしばらく彷徨った末に \(15\) のコラッツ兄弟である \(61\) へ戻ってくる。 この関係を明らかにできれば、\(15\) が収束するなら \(31,63\) どちらも収束するということになる。

上位へ行ってしまう数や行ってしまった数のうち \(47\) は \(31\) の軌道上に \(95\) は \(63\) の軌道上にある。 \(55\) の変換先 \(83\) は その先を辿ってみると \(31\) の放浪の旅に接続している。 上位の世代では \(31\) に相当する数から \(63\) に相当する数の間が広くなり、\(55\) に相当する数が増える。 これを一般化して確認する必要がある。 放浪の旅は、上位の世代へ行ってしまったものを拾っていく旅になっていることを明らかにできれば、 \(31,63\) が収束するなら上位の世代へ行ってしまうものも収束するということになる。

と、言う訳で、数学的帰納法へ帰着させるなら、

(1)

図8,9,10,11で行き先（下位の世代へ行くか上位の世代へ行くか）が決まり、この中で循環しないこと。

(2)

\(\mbox{all}~1_{(2)}\) について、下位の世代のコラッツ双子と上位の世代のコラッツ双子の関係を明らかにすること。

(3)

上位の世代に行くものは、\(\mbox{all}~1_{(2)}\) の放浪の旅に合流していること。

  ふぅ。やっと、基本のガジェットと、場合分けと、証明すべきこと、が出揃った。
(1)は疑似乱数（線形合同法）の網羅条件に似ているような気がする。 \(\TeX\)のクヌースなら循環しない条件を示してくれそう。 その条件が任意の世代で一般に成立しているかが、コラッツ問題のキモであり一番難しいところになるのかも知れない。
(2)は可能性はありそう。 旅の途中で、他の系列に引っ掛かって仕舞うようなら、 \(31\) が \(15\) へ還ってくるといった、面白い挙動をするハズがない。
(3)は別の言い方をすると、1〜1は一直線、3はその双子。3〜7は一直線、15はその双子。しかし15〜31は双子の同期側を2回選択しており一直線でない。 3で割り切れたらといった括りでもなさそう。このルールを見つけたい

  ところで何故に世代？ 階層とかでいいじゃん。 いや、何となく元素の周期表に似ていると思いません？ きっとコラッツ問題は虚数の世界で素粒子の世代に繋がっているんだぁ〜って思いません？ 思わない。そうですか、そうですね。 スミマセン、私が悪かったです。ゴメンナサイ

prev |  1 |  2 |  3 |  4  |  5 |  6 |  7 |  next