prev |  1 |  2 |  3 |  4 |  5  |  6 |  7 |  next

漸化式 \(x_{i+1}=3x_i+1\) の一般項

  定石通りに一般項を導く。漸化式 \begin{align} x_{i+1}=3x_i+1 \end{align} に対し特性方程式 \begin{align} c=3c+1 \end{align} を満たす \(c\) が存在すれば（漸化式と特性方程式の差をとって） \begin{align} x_{i+1}-c=3(x_i-c) \end{align} の等比数列が成り立つ。\(c\) を解くと \begin{align} c=-\frac{1}{2} \end{align} なのでこれを代入し \begin{align} 2x_{i+1}+1=3(2x_i+1) \end{align} より一般項は \begin{align} 2x_n+1=(2x_0+1)3^n \end{align} となる。 特に \(x_0=0\) の場合は \begin{align} 2x_n+1=3^n \end{align} \begin{align} 2x_n=3^n-1=(3-1)(3^{n-1}+3^{n-2}+\cdots+3^1+3^0) \end{align} \begin{align} x_n=3^{n-1}+3^{n-2}+\cdots+3^1+3^0 \end{align} \(3\) のべき級数になる。項が偶数個の場合は \begin{align} \begin{array}{rl} x_6&=3^5+3^4+3^3+3^2+3^1+3^0 \\ &=3^4(3+1)+3^2(3+1)+3^0(3+1) \\ &=(3+1)(3^4+3^2+3^0) \\ &=4(9^2+9^1+9^0) \\ \end{array} \end{align} 半分の長さの \(9\) のべき級数になる。

  コラッツ掃出しは上位の値を末尾の連続1の数だけ \(3x+1\) するが、 一般項で掃出しのプロセスをショートカットできる。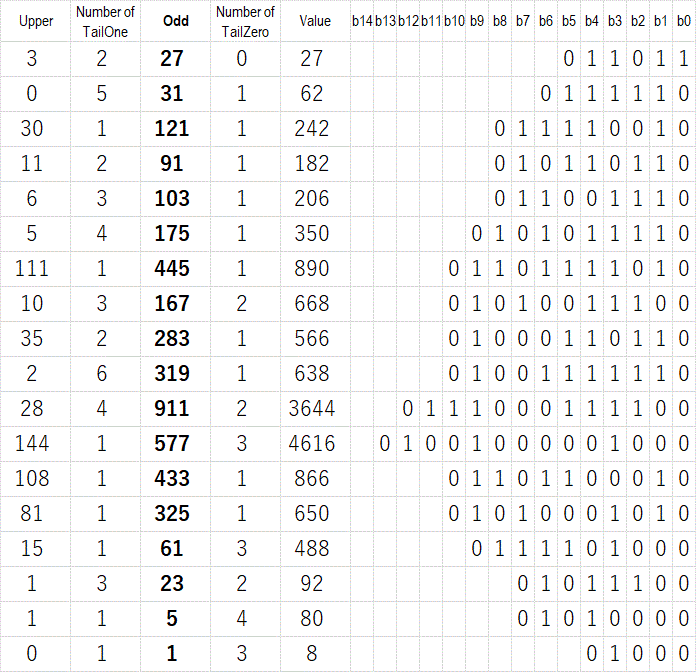

図14：初期値 \(27\) からの変遷 （ダウンロードはこちら）

図4より図14の方が表が短くなった。

  \(x_0=0\) の場合のビットパターンを掲載しておく。
末尾のビット変化は \(01_{(2)}\), \(00_{(2)}\) の交互になっている。

        
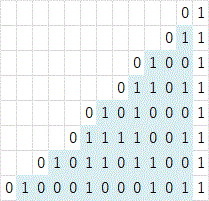図15：\(x_0=0\) , \(x_{i+1}=3x_i+1\) のビット変化
参考 \(y_0=1\) , \(y_{i+1}=3y_i\) のビット変化（青着色部が一致）

  以上まとめると、桁数 \(n\) の \(\mbox{all}~1_{(2)}\) は 桁数 \(n\) の \(\mbox{all}~1_{(3)}\) になる。
これが偶数桁の場合は半桁の \(\mbox{all}~1_{(9)}\) になる。 奇数桁の場合は末尾が必ず \(01_{(2)}\) であり、もう1回コラッツ変換するので 結局で偶数桁になり、やはりその半桁の \(\mbox{all}~1_{(9)}\) になる。
1行目に初期値で、縦方向にコラッツ掃出し結果を示す。

図16：\(\mbox{all}~1_{(2)}\) のコラッツ掃出し結果

表中の \(2\) で何回割るのかは、 偶数桁の \(\mbox{all}~1_{(3)}\) は \(3+1\) で括って \(\mbox{all}~1_{(9)}\) になり、 偶数桁の \(\mbox{all}~1_{(9)}\) は \(9+1\) で括って \(\mbox{all}~1_{(81)}\) になり、 …、 という周期になっている （尚 \(2\) で割ったら \(\mbox{all}~1_{(81)}\) ではなく \(5\times\mbox{all}~1_{(81)}\) 即ち \(\mbox{all}~5_{(81)}\) になるので注意） \(3+1\) は \(2^2\) だが、その先の \(9+1\), \(81+1\), \(\cdots\) は偶数であるが因数 \(2\) はひとつ。 末尾2bitに着目\(\pmod{4}\)すると \(3\equiv11_{(2)}\), \(9\equiv01_{(2)}\), \(81\equiv01_{(2)}\), \(\cdots\) で \((01_{(2)})^2\equiv01_{(2)}\) なのでこれに \(1\) を足すと偶数。因数 \(2\) で除すと末尾 \(1_{(2)}\) で奇数。よって因数 \(2\) はひとつだけ。 従って \(2\) で割る回数は上述の規則が続く。

  \(\mbox{all}~1_{(9)}\) になることは判った。 奇数化した結果がコラッツ掃出し過程の数と循環していないかの確認が必要だがひとまず放置する。 何処へ到達するかが解れば、循環しなかったことの逆証明になるだろう。
これで \(31\) から \(15\) の距離は \(91\) から \(61\) の距離に縮まった。

  ちなみに、数学で距離というと別の意味になりそうだが、深い意味はありません。
難しい論法は私には分からん。挟み撃ちくらいは使うことになるかもなぁ…
遅蒔きながら、図書館でコラッツ問題の本でも読むか…
自分が考えつく程度のことは全部既知公知なんだろうなぁ〜

コラッツ掃寄せ

  末尾の1が単独で区切りの0が連続の場合、 末尾の1をスイープアウトすると繰り上がりの1が残り、 末尾の桁が上がっていく。 上位は \(3x_i\) となり、その中の上位部分（青着色）は \(3x_i+1\) となる。 区切りの連続0が減っていき、上位と末尾の1が接近する。 （以下「コラッツ掃寄せ」と呼称する）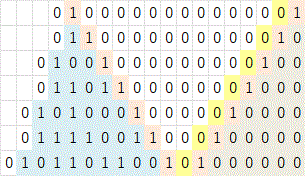

図17：孤立した最下位の1のビット変化

  これにより具体的な計算の場合には、 途中経過を端折ることがことができる。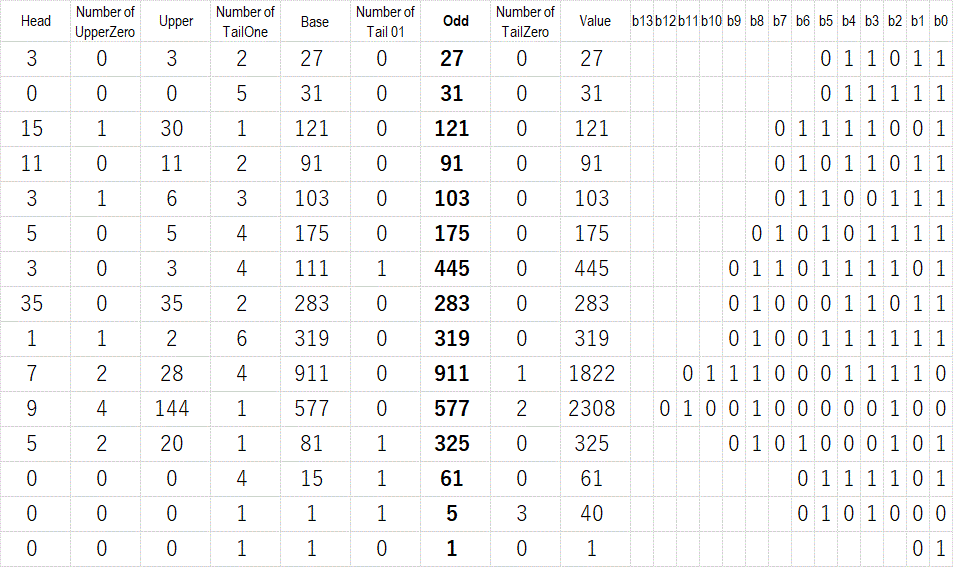
末尾の連続0を削除する。即ち奇数化する。
末尾の連続01を削除する。但し基本の奇数を残す。
末尾の1が単独で、区切りの0が連続なら、コラッツ掃寄せする。
そうでなければ、コラッツ掃出しする。

図18：初期値 \(27\) からの変遷 （ダウンロードはこちら）

図14より図18の方が表がちょっとだけ短くなった。 これで \(91\) から \(61\) の距離が少しだけ縮まった。 一般の証明には繋がらないが考察の助けにはなるかも知れない。

  コラッツ掃寄せにもコラッツ双子がある。 区切りの連続0の数がひとつ違いで \(2x-1\) の関係である。

    
図19：コラッツ掃寄せのコラッツ双子

prev |  1 |  2 |  3 |  4 |  5  |  6 |  7 |  next