prev |  1 |  2  |  3 |  4 |  5 |  6 |  7 |  next

\(x\) を \(m\) で何回割れるか

  記述のため、整数 \(x\) に因数 \(m\) が何個含まれるかを返す関数 \(\mbox{fctr}_{m}x\) を導入する。 \(x=m^n\) のときは \(\mbox{fctr}_{m}x=\log_{m}x=n\) であり、整数版の \(\log\) である。

因数分解を意図しているが、素因数分解を意図するものではない。
既存の同等な関数あるいは他の適切な記法があれば申し訳ない。
\(\mbox{約数}\times\mbox{因数}^\mbox{指数}\)という表現をしたいだけです（浮動小数点ではないが）

桁下げ有り操作

  奇数の変遷だけ追いたい。
\(/2\) の過程はショートカットする（計算が減る訳ではない）

桁下げ無し操作

  奇数化すると、値の連続性が無くなり判りにくい。
\(/2\) をやめてしまい \(+1\) に代えて \(+2^m\) にする（計算が減る訳ではない）

  桁下げ有り操作と桁下げ無し操作を2進表示で並べて示す。

        
図2：2進表示した桁下げ有り操作と桁下げ無し操作

末尾の連続0（グレーアウト部分）を取り除くと同一ビットパターンである。 つまり、表示が変わってもやっていることは同じである。

  コラッツ数列は、膨張過程と収縮過程を繰り返し最後に \(1\) に落ち着くが、 この様子が雹の成長過程に似ており雹モデルと言われる。
桁下げ無しは、桁が揃い、値が連続し、場合によっては判りやすい。 （雹モデルでなくなる訳ではない）

コラッツ掃出し

  \(3x+1\) の演算をそのままでは理解しにくいので \(2x+x+1\) に分解する。 2進で \(2x\) は \(x\) を1ビット左シフトである。 \(x=1\cdots1_{(2)}\) について見てみる。 図で上段から順に \(2x\) , \(x\) , \(1\) である。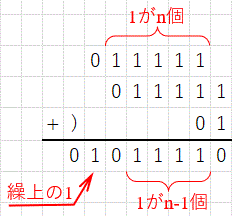

図3：末尾 \(1\cdots1_{(2)}\) についての \(3x+1\)

\(1\cdots1_{(2)}\) について \(3x+1\) は末尾の1をひとつ減らす効果がある。
代わりに繰上げの1が生じる。

奇数は2進で、末尾の連続1、区切りの0、上位の値、に区分できる。 コラッツ変換は、末尾の1をひとつ減らし、上位は3倍+繰上げの1になる。 （以下「コラッツ掃出し」と呼称する）

変遷

  次の図は \(27\) からの桁下げ無し操作の結果の変遷である。
赤着色は末尾の連続1、黄着色は区切りの0、青着色は上位の値である。

図4：初期値 \(27\) からの変遷 （ダウンロードはこちら）

  最上位がほぼ一定のペースで桁上がりしている。 これが桁下げ無し操作である。 右側の0で埋め尽くされグレーアウトしている領域が、 桁下げ有り操作では2で割って取り除いている領域である。

  先の考察の通り、末尾の連続1が減り、上位の値が \(u_{i+1}=3u_i+1\) になっている。 コラッツ掃出しが終了すると、上位の値だった部分が新たな末尾となり次のコラッツ掃出しが始まる。

  最上位の桁上がりを末尾の掃出しが追っている。 末尾の掃出しより、上位の値のビット長の伸びが勝っている。 奇数部分の全長は膨張していくが、膨張しきったところで連続消去が発生し、終了している。

prev |  1 |  2  |  3 |  4 |  5 |  6 |  7 |  next